Answer:
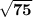
Explanation:
Given
A
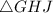 in which
in which
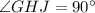
Hypotenuse = 10
Length of another side = 5
To find:
HJ = ?
Solution:
Kindly refer to the image attached in the answer area.
We know that there are only 3 sides in a triangle.
We are given hypotenuse is 10.
i.e. GJ = 10
To find HJ, Base = ?
So, we are given the side length of GH, perpendicular i.e. 5.
Kindly refer to attached image for further details.
Let us use Pythagorean theorem here.
According to Pythagorean theorem:
