Answer:
121
Explanation:
Given data as per the question
Standard deviation =
 = 840
= 840
Margin of error = E = 150
Confidence level = c = 95%
For 95% confidence, z = 1.96
based on the above information, the minimum number of clients surveyed by the travel agent is
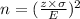
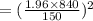
= 120.47
= 121
hence, the 121 number of clients to be surveyed
Therefore we applied the above formula to determine the minimum number of clients