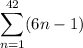Answer:
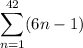
Explanation:
Given:
To find:
- Summation notation of the given series
Summation Notation:
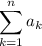
Where n is the number of terms and
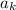 is general term.
is general term.
First, determine what kind of series it is, there are two main series that everyone should know:
A series that has common difference.
A series that has common ratio.
If you notice and keep subtracting the next term with previous term:
Two common difference, we can in fact say that the series is arithmetic one. Since we know the type of series, we have to find the number of terms.
Now that brings us to arithmetic sequence, we know that first term is 5 and last term is 251, we’ll be finding both general term and number of term using arithmetic sequence:
Arithmetic Sequence
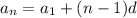
Where
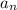 is the nth term,
is the nth term,
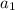 is the first term and
is the first term and
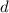 is the common difference:
is the common difference:
So for our general term:
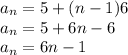
And for number of terms, substitute
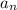 = 251 and solve for n:
= 251 and solve for n:
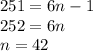
Now we can convert the series to summation notation as given the formula above, substitute as we get: