Answer:
![g(x)=4\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/ewtk6qlhvlfqbj17fuorb46k5qmmotuyit.png)
Explanation:
We can see that the curve has not been translated horizontally or vertically, nor has it been reflected in either axis. Therefore, g(x) is a stretch:


Parent function
![f(x)=\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/bpa3vuuo5dtqkg0vqcw69omticpmu0m3k9.png)
![\implies g(x)=a\:f(x)=a\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/9tnl1ftliecgykeeoxxndfzriuchuj4zne.png)
![\textsf{or}\quad g(x)=f(ax)=\sqrt[3]{ax}](https://img.qammunity.org/2023/formulas/mathematics/college/b4hu1ps2p8n3oysyldz5lau510axolof6l.png)
From inspection of the graph:
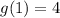
Therefore:
![\implies a\sqrt[3]{1}=4](https://img.qammunity.org/2023/formulas/mathematics/college/i17sau6xju4n7euflwalmzt0pzjdaoiych.png)
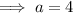
![\implies g(x)=4\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/xs1hswmxy020ljpc7c7ix04zpx5fd0xlcb.png)
Or:
![\implies \sqrt[3]{a(1)}=4](https://img.qammunity.org/2023/formulas/mathematics/college/sq8c1nq2mdf7eka4lo4fr3reppekz65n9z.png)
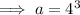

![\implies g(x)=\sqrt[3]{64x}](https://img.qammunity.org/2023/formulas/mathematics/college/fs1l6jplp16dorlq4fb7t46lnnl3u8puxx.png)
![\implies g(x)=\sqrt[3]{64}\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/eayt5e4qr8nkhw0xpup7jjiueho3d6i9rs.png)
![\implies g(x)=4\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/xs1hswmxy020ljpc7c7ix04zpx5fd0xlcb.png)
Therefore, the translated function is:
![g(x)=4\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/ewtk6qlhvlfqbj17fuorb46k5qmmotuyit.png)