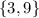Question

Which numbers in set ={,,,,,,,,,}eh equals left brace 1 comma 2 comma 3 comma 4 comma 5 comma 6 comma 7 comma 8 comma 9 comma 10 right brace are elements in both the subset of odd numbers and the subset of multiples of 3?

Answer 1

the answer is:
`\{3, 9\}`

Explanation:

Given a set:

Let S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Two subsets,

One subset of odd numbers:

A = {1, 3, 5, 7, 9, 11, 13, 15, 17, ......}

Other subset of multiples of 3:

B = {3, 6, 9, 12, 15, .....}

To find:

Which number in set S are elements in both A and B.

So, we need to find intersection of A and B provided the number is between 1 to 10 (1 to 10 are the elements of S).

First of all, let us have intersection (i.e. common elements) of A and B:

`A\cap B = \{3, 9, 15, 21, ......\}`

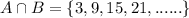
Now, the numbers between 1 to 10 are:

`\{3, 9\}`

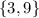
So, the answer is:
`\{3, 9\}`