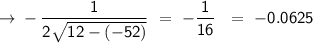Question

Find the slope of the tangent line to f(x) = √(12-x) at x = -52

Write your answer as an integer or a fraction

Please give a thorough answer, this is practice for finals and I have forgotten how to do this.

Answer 1

slope: -0.0625

Step-by-step explanation:

To find slope of a function, we have to find the derivative of the function.

• Here given the function: f(x) = √(12-x)

Start deriving the equation:

`\rightarrow \sf (dy)/(dx) = (d)/(dx) ( √(12-x) )`

`\rightarrow \sf (dy)/(dx) = (d)/(dx) ( (12-x)^{(1)/(2) }} )`

`\rightarrow \sf (dy)/(dx) = (1)/(2) ( (12-x)^{(1)/(2)-1 }} )(-1)`

`\rightarrow \sf (1)/(2√(12-x))\left(-1\right)`

`\rightarrow \sf -(1)/(2√(12-x))`

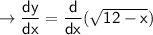
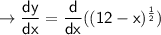
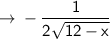
`\bold{\star}` Tangent/Parallel Line Has Same Slope

To find slope at x = -52, simplify insert x = -52 in derivative we found

`\rightarrow \sf -(1)/(2√(12-(-52))) \ = \ -(1)/(16) \ \ = \ -0.0625`

Answer 2

`-(1)/(16)` or -0.0625

Step-by-step explanation:

To find the slope of the tangent line at a point, differentiate the function (using the chain rule for this particular function), then input the x-coordinate of the point into the first derivative.

`\begin{aligned}f(x) & = √(12-x)\\& = (12-x)^{(1)/(2)}\\\\\implies f'(x) & =(1)/(2)(12-x)^{-(1)/(2)} \cdot -1\\& = -(1)/(2√(12-x))\end{aligned}`

Therefore, the slope of the tangent line to f(x) at x = -52 is:

`\begin{aligned}f'(-52) &=-(1)/(2√(12-(-52)))\\\\&=-(1)/(2√(64))\\\\&=-(1)/(2 \cdot 8)\\\\&=-(1)/(16)\\\\&=-0.0625\end{aligned}`