Question

Find the equation of the tangent line to g(x) = 4x² + 6x at x = 0
Simplify any fractions

Answer 1

y = 6x

Explanation:

Given:

`\displaystyle \large{g(x)=4x^2+6x}`

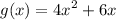
To find:

• Tangent line equation at x = 0

First, derive the equation using power rules. Here are some power rules formula:

Power Rules

`\displaystyle \large{f(x) = x^n \to f'(x)=nx^(n-1)}\\\\\displaystyle \large{f(x)=kx^n \to f'(x)=knx^(n-1) \quad \tt{(k \ \ is \ \ constant.)}}\\\\\displaystyle \large{f(x)=k \to f'(x)=0 \quad \tt{(k \ \ is \ \ constant.)}`

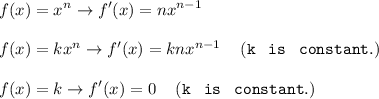
Apply power rules:

`\displaystyle \large{g'(x)=4(2)x^(2-1)+6(1)x^(1-1)}\\\\\displaystyle \large{g'(x)=8x+6}`

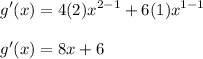
Derivative Definition

• Derivative simply means slope or gradient at any points (x,y) and it is also rate of changes.

Since we want to find the slope at x = 0 (so that the line will be tangent to this point) then substitute x = 0 in g’(x):

`\displaystyle \large{g'(0)=8(0)+6}\\\\\displaystyle \large{g'(0)=6}`

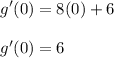
Now we have slope = 6 at x = 0. Next, find y-value at x = 0, simply substitute x = 0 in g(x) to find y-value:

`\displaystyle \large{g(0)=4(0)^2+6(0)}\\\\\displaystyle \large{g(0)=0}`

So we have point (0,0) which is origin point. Before we head to next step, let’s review on what we have:

• Slope at x = 0 is 6
• Point (0,0)

Next, we use point-slope form to create the equation and convert to slope-intercept form:

Point-Slope

`\displaystyle \large{y-y_1=m(x-x_1)}`

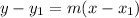
Determine:

• 
  `\displaystyle \large{m=6}`
• 
  `\displaystyle \large{(x_1,y_1)=(0,0)}`

Therefore:

`\displaystyle \large{y-0=6(x-0)}\\\\\displaystyle \large{y=6x}`

Therefore, the equation of tangent line to the parabola at x = 0 is y = 6x

Answer 2

y = 6x

To find equation,

1) Find Derivative

2) Find the slope at x

3) Find coordinates

Lets first Derive The Equation

`\sf \rightarrow y = 4x^2 + 6x`

`\sf \rightarrow (dy)/(dx) = (2)4x^(2-1) + (1)6x^(1-1)`

`\sf \rightarrow (dy)/(dx) = 8x + 6`

Secondly find Slope at x = 0

`\sf \rightarrow (dy)/(dx) = 8(0) + 6`

`\sf \rightarrow (dy)/(dx) = 6` Yep so the slope(m) is 6.

Recall, tangent line has the same slope.

Now third step is to find coordinates

At x = 0, y = 4x² + 6x ⇒ y = 4(0)² + 6(0) = 0
`\star` so coordinates: (0, 0)

Equation:

• y - y₁ = m(x - x₁)

• y - 0 = 6(x -0)

• y = 6x