Answer:
x = 8
Explanation:
To find the value of x when y = 18 we must first find the relationship between them.
The statement
y varies inversely as x is written as
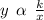
where k is the constant of proportionality
From the question when
y = 6
x = 24
Substitute the values into the above equation
That's
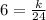
Cross multiply
That's
k = 24(6)
k = 144
So the formula for the variation is
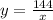
When
y = 18
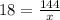
Cross multiply
18x = 144
Divide both sides by 18
x = 8
Hope this helps you