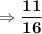Question

PLEASE FAST 40 POINTS

A box contains four tiles, numbered 1,4.5, and 8 as shown.

Kelly randomly chooses one tile, places it back in the box, then chooses a second tile.

What is the probability that the sum of the two chosen tiles is greater than 7?

A. 1/4
B. 5/16
C. 2/3
D. 11/16

Answer 1

Answer:11/16

Step-by-step explanation:i took the test

Answer 2

`\bold{(11)/(16)}`

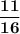
Explanation:

Given four tiles with numbers:

1, 4, 5 and 8

Tile chosen once and then replaced, after that another tile chosen:

All possibilities are:

{(1, 1) ,(1, 4) ,(1, 5) ,(1, 8)

(4, 1) ,(4, 4) ,(4, 5) ,(4, 8)

(5, 1) ,(5, 4) ,(5, 5) ,(5, 8)

(8, 1) ,(8, 4) ,(8, 5) ,(8, 8) }

Total number of possibilities = 16

When the sum is greater than 7, the possibilities are:

{(1, 8)

(4, 4) ,(4, 5) ,(4, 8)

(5, 4) ,(5, 5) ,(5, 8)

(8, 1) ,(8, 4) ,(8, 5) ,(8, 8) }

Number of favorable cases = 11

Formula for probability of an event E is:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

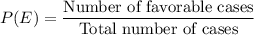
Hence, the required probability is:

`\Rightarrow \bold{(11)/(16)}`