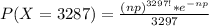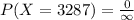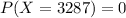Answer:
a
normal approximation not appropriate in this instance because
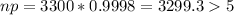
and
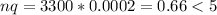
b
The probability is
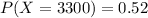
c
The probability is
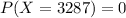
Explanation:
From the question we are told that
The sample size is
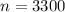
The chance of liking blueberry pie is
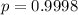
The chance of not liking blueberry pie is
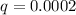
For normal approximation is possible if
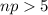 ,
,
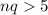
Now let test
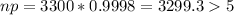
and
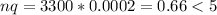
The probability that all 3300 people will say they like blueberry pie is mathematically represented as
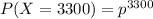
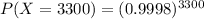
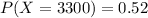
The probability that 3297 of the people will say that they like blueberry pie is mathematically represented as