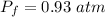Answer:
The pressure is
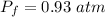
Step-by-step explanation:
From the question we are told that
The volume of Ne is
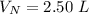
The volume of CO is

The pressure of
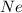 is
is
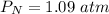
The pressure of CO is
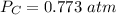
The number of moles of Ne present is evaluated using the ideal gas equation as
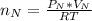
=>

The number of moles of CO present is evaluated using the ideal gas equation as

=>
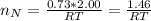
The total number of moles of gas present is evaluated as
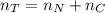
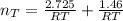
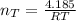
The total volume of gas present when valve is opened is mathematically represented as
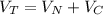
=>
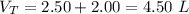
So
From the ideal gas equation the final pressure inside the system is mathematically represented as
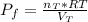
=>
![P_f = ([(4.185)/(RT) ] * RT )/( 4.50)](https://img.qammunity.org/2021/formulas/chemistry/high-school/dpfxa5yz6nn0znpfnqvhqyb20j54gzbho3.png)
=>