Question

The table below shows the amount paid for different numbers of items. Determine if this relationship forms a direct variation. Verify your answer.

Answer 1

Answer/Step-by-step explanation:

Direct variation occurs when a variable varies directly with another variable. That is, as the x-variable increases, the y-variable also increases.

The ratio of between y-variable and x-variable would be constant.

Direct variation can be represented by the equation,
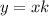`y = xk`, where k is a constant. Thus,

`(y)/(x) = k`

From the table given, it seems, as x increases, y also increases. Let's find out if there is a constant of proportionality (k).

Thus, ratio of y to x,
`(0.50)/(1) = 0.5`

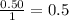
k = 0.5.

If the given table of values has a direct variation relationship, then, plugging in the values of any (x, y), into
`(y)/(x) = k`, should give us the same constant if proportionality.

Let's check:

When x = 2, and y = 1:

`(y)/(x) = k`,

`(1)/(2) = 0.5`,

When x = 3, y = 1.5:

`(1.5)/(3) = 0.5`,

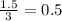When x = 5, y = 2.50:

`(2.5)/(5) = 0.5`,

The constant of proportionality is the same. Therefore, the relationship forms a direct variation.