Answer:
T' = 2T
Step-by-step explanation:
The time period of a simple pendulum is given by the relation as follows :

l is length of the pendulum
g is acceleration due to gravity
If the length is increased four time, new length is l' = 4l
So,
New time period is :
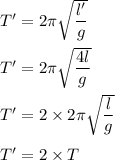
So, the new time period is 2 times of the initial time period.