Question

Heights of certain plants at a nursery are normally distributed with a mean of 52.5 centimeters and a standard deviation of 7.2 centimeters. If their z-scores are greater than 2.25, the plants are displayed in the main lobby. To the nearest centimeter, what is the minimum required height for this type of plant to be displayed in the main lobby? Question 7 options: 68 cm 55 cm 69 cm 56 cm

Answer 1

The correct option is;

69 cm

Explanation:

The z-score, or standard score is a measure of how far a data is from the mean

The z-score, is given by the relation;

`z = (x- \mu)/(\sigma)`

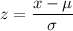
Z = Standard score

x = Value observed

μ = The mean height of the plants = 52.5 cm

σ = Standard deviation = 7.2 cm

Given that the z-score = 2.25, we have;

`2.25 = (x- 52.5)/(7.2)`

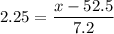
Therefore, x = 7.2 × 2.25 + 52.5 = 68.7 cm ≈ 69 cm

Therefore, the minimum required height for this type of plant to be displayed in the main lobby is 69 cm.