Question

The number of peanuts in bags is normally distributed with a mean of 184.7 peanuts and a standard deviation of 3.3 peanuts. What is the z-score of a bag containing 178 peanuts? Question 6 options: negative 1.42 negative 2.03 negative 2.49 negative 1.65

Answer 1

The z-score of a bag containing 178 peanuts is -2.03.

Explanation:

A z-score is a normally distributed value with mean 0 and standard deviation 1. The distribution of these z-scores is known as the standard normal distribution.

The formula to compute z-score is:

`z=(x-\mu)/(\sigma)`

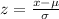
The information provided is:

x = 178

μ = 184.7

σ = 3.3

Compute the z-score of a bag containing 178 peanuts as follows:

`z=(x-\mu)/(\sigma)`

`=(178-184.7)/(3.3)\\\\=-2.03`

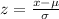
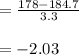
Thus, the z-score of a bag containing 178 peanuts is -2.03.