Answer:
The polygon has 10 sides
Explanation:
One of the interior angles of a polygon can be found using the formula
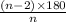
where n is the number of sides of the polygon
From the question
One of the interior angles = 144
To find the number of sides substitute this value into the above formula and solve for n
That's

Cross multiply
We have
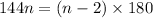
Expand the terms in the bracket
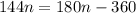
Group like terms
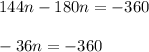
Divide both sides by - 36
That's
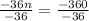
We have the final answer as
n = 10 sides
Hope this helps you