Question

HCF of x minus 2 and X square + X - 6 ​

Answer 1

x - 2

Explanation:

by factorization method

1) x - 2

2) x^2 + x - 6

by splitting method

x^2 + 3x - 2x - 6

taking separate common from the first two terms and last two terms

x(x + 3) - 2(x + 3)

now writing x+3 once and the other term to get the right answer

(x + 3)(x - 2)

in both parts just see the similar term and write it as HCF

HCF= x - 2

and the second method by which you can get this answer is division method

Answer 2

`\boxed{ \sf{ \bold{ \huge{ \boxed{x - 2}}}}}`

Explanation:

`\sf{x - 2} \: and \: { {x}^(2) + x - 6}`

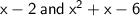
To find the H.C.F of the algebraic expressions, they are to be factorised and a common factor or the product of common factors is obtained as their H.C.F

Let's solve

First expression = x - 2

Second expression = x + x - 6

Here, we have to find the two numbers which subtracts to 1 and multiplies to 6

= x + ( 3 - 2 ) x + 6

Distribute x through the parentheses

= x + 3x - 2x + 6

Factor out x from the expression

= x ( x + 3 ) - 2x + 6

Factor out -2 from the expression

= x ( x + 3 ) - 2 ( x + 3 )

Factor out x+3 from the expression

= ( x + 3 ) ( x - 2 )

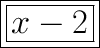
Here, x - 2 is common in both expression.

Thus, H.C.F = x - 2

Hope I helped!

Best regards!!!