Answer:
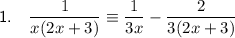
![\textsf{2a.} \quad y= \sqrt[3]{(5x)/(2x+3)}](https://img.qammunity.org/2023/formulas/mathematics/college/ofh0326u97dv4tjpqn82ozg9akn4s3glc2.png)
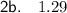
Explanation:
Question 1
A fraction with more than one linear factor in the denominator can be decomposed into partial fractions. This means writing it as a sum of two or more simpler fractions, making it easier to integrate, manipulate, or solve equations involving the original fraction.
Given fraction:
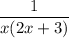
Write out the expression as an identity:
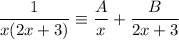
Add the partial fractions:
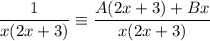
Cancel the denominators from both sides of the identity, so the numerators are equal:
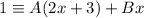
Rearrange:
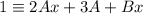
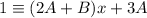
Solve the unknown parameters A and B by plugging in the real roots of the denominator of the original fraction: x = 0 and x = -3/2.
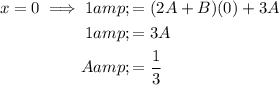
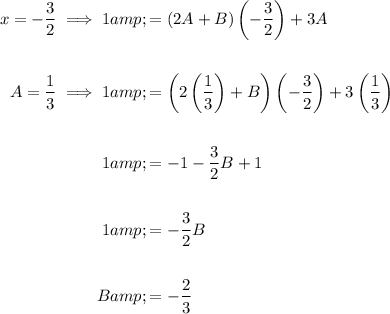
Finally, replace A and B in the original identity to express the given fraction as partial fractions:
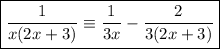

Question 2a
Given differential equation:
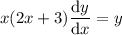
To solve the differential equation, first move all the terms containing y to the left-hand side, and all the terms containing x to the right-hand side, and split up the dy/dx:
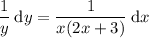
Now integrate both sides:
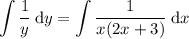
Substitute the found partial fractions from the previous question:
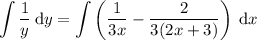
Simplify by separating the integrals and taking the constants outside:
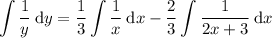
Integrate:
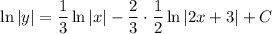
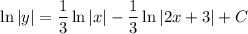
To find the value of C, substitute the given parameters of y = 1 when x = 1:
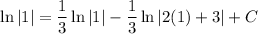
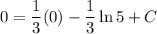
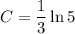
Therefore:
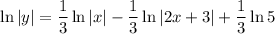
Factor out 1/3 from the right side of the equation:
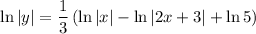
Use log rules to simplify the right side of the equation:
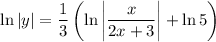
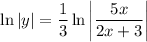
![\ln|y|=\ln \sqrt[3]\left](https://img.qammunity.org/2023/formulas/mathematics/college/vv4xd1uwha3m558ikmz4t8v0dfpqa539xb.png)
Therefore:
![y= \sqrt[3]{(5x)/(2x+3)}](https://img.qammunity.org/2023/formulas/mathematics/college/5cuqay68pe9gkizjue2jn1o2kto4h83i25.png)

Question 2b
To calculate the value of y when x = 9, substitute x = 9 into the equation for y found in question 2a:
![\begin{aligned}x=9 \implies y&= \sqrt[3]{(5(9))/(2(9)+3)}\\\\&= \sqrt[3]{(45)/(18+3)}\\\\&= \sqrt[3]{(45)/(21)}\\\\&= \sqrt[3]{(15 \cdot 3)/(7 \cdot 3)}\\\\&= \sqrt[3]{(15)/(7)}\\\\&= 1.28923198...\\\\&=1.29\; \sf (2\;d.p.)\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/7lcm1pzh8y8i03y1lhhrioj32eucetcpa1.png)
Therefore, the value of y when x = 9 is 1.29 to two decimal places.