Question

Pls help me .question no 14

Answer 1

Question 14, Part (i)

Focus on quadrilateral ABCD. The interior angles add to 360 (this is true for any quadrilateral), so,

A+B+C+D = 360

A+90+C+90 = 360

A+C+180 = 360

A+C = 360-180

A+C = 180

Since angles A and C add to 180, this shows they are supplementary. This is the same as saying angles 2 and 3 are supplementary.

==================================================

Question 14, Part (ii)

Let

x = measure of angle 1

y = measure of angle 2

z = measure of angle 3

Back in part (i) above, we showed that y + z = 180

Note that angles 1 and 2 are adjacent to form a straight line, so we can say

x+y = 180

-------

We have the two equations x+y = 180 and y+z = 180 to form this system of equations

`\begin{cases}x+y = 180\\y+z = 180\end{cases}`

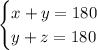
Which is really the same as this system

`\begin{cases}x+y+0 = 180\\0+y+z = 180\end{cases}`

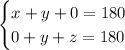
The 0s help align the y terms up. Subtracting straight down leads to the equation x-z = 0 and we can solve to get x = z. Therefore showing that angle 1 and angle 3 are congruent. We could also use the substitution rule to end up with x = z as well.