Answer:
P- value = 0.0069
Explanation:
Given that :
sample size n = 1600
The sample proportion
 = 0.42
= 0.42
The population proportion p = 0.39
The null hypothesis and the alternative hypothesis can be expressed as:
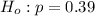
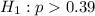
The test statistics can be computed as follows:

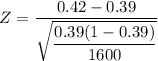
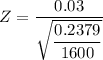
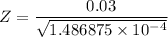

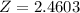
Z
 2.46
2.46
Determine the P-value of the test statistic.
The P- value = P(Z >
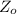 )
)
P- value = 1 - P( Z ≤ 2.46)
Using the Excel Function ( = NORMSDIST (2.46))
P- value = 1 - 0.993053
P- value = 0.006947
P- value = 0.0069 to four decimal places