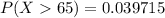Complete Question
The mean height of women in a country (ages 20-29) is 64.4 inches. A random sample of 75 women in this age ground is selected. what is the probability that the mean height for the sample is greater than 65 inches? assume
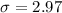
Answer:
The value is
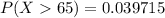
Explanation:
From question we are told that
The mean is
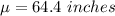
The sample size is
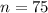
The probability that the mean height for the sample is greater than 65 inches is mathematically represented as
![P(X > 65) = P[(X - \mu )/( \sigma_(\= x) ) > (65 - 64.4 )/( \sigma_(\= x) ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/usj0htwchnbk0qjhjwtg4xi2m9qp8tgj06.png)
Where
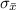 is the standard error of mean which is evaluated as
is the standard error of mean which is evaluated as
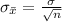
=>
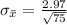
=>
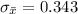
Generally

![P(X > 65) = P[Z> (65 - 64.4 )/(0.342 ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/h5yipp898w19c87gqoko7r5nvlno8w7v13.png)
So
![P(X > 65) = P[Z >1.754 ]](https://img.qammunity.org/2021/formulas/mathematics/college/hawjvtpy7cyuwb39sg439pd305y66wwysc.png)
From the z-table the value of
![P(X > 65) = P[Z >1.754 ] = 0.039715](https://img.qammunity.org/2021/formulas/mathematics/college/z0ifcdogkro2wltatn6hw4rkz2hmqscxi5.png)