Question

A race-car drives around a circular track of radius RRR. The race-car speeds around its first lap at linear speed v_iv i ​ v, start subscript, i, end subscript. Later, its speed increases to 4v_i4v i ​ 4, v, start subscript, i, end subscript. How does the magnitude of the car's centripetal acceleration change after the linear speed increases

Answer 1

Answer and Explanation: Centripetal Acceleration is the change in velocity caused by a circular motion. It is calculated as:

`a_(c)=(v^(2))/(r)`

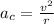
v is linear speed

r is radius of the curve the object in traveling along

For its first lap:

`a_(c)_(1)=(v_(i)^(2))/(R)`

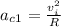
After a while:

`a_(c)_(2)=((4v_(i))^(2))/(R)`

`a_(c)_(2)=(16v_(i)^(2))/(R)`

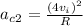
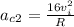
Comparing accelerations:

`(a_(c)_(2))/(a_(c)_(1))=(16.v_(i)^(2))/(R).(R)/(v_(i)^(2))`

`(a_(c)_(2))/(a_(c)_(1))=(16.v_(i)^(2))/(R).(R)/(v_(i)^(2))`

`(a_(c)_(2))/(a_(c)_(1))=16`

`a_(c)_(2)=16a_(c)_(1)`

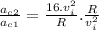
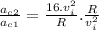
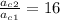
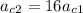
With linear speed 4 times faster, centripetal acceleration is 16 times greater.