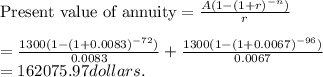Answer:
162075.97 dollars.
Step-by-step explanation:
The time period of annuity = 15 years
Annuity amount = $1300 per month
The interest rate for the first six-year = 10%
Monthly interest rate = 10% / 12 = 0.83%
Thus number pf periods = 6 * 12 = 72
Interest rate for another 9 years = 8%
Monthly interest rate = 8% / 12 = 0.67%
Number of period = 8 * 12 = 96
Use the below formula to find the present value of the annuity.