Answer:
Step-by-step explanation:
Given that:
The argon atoms are excited into an excited state before emitting the 488.0 nm laser.
the energy of the first ionization energy of argon is 1520 kJ mol-1.
SInce 1 eV = 96.49 kJ/mol
Therefore, the energy of the first ionization energy of argon in eV is = ( 1520/ 96.49) eV
= 15.75 eV
To find where the energy level of the excited state lies below the vacuum energy level, let's first determine, the energy liberated by using planck expression.
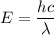
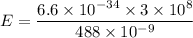
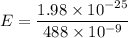
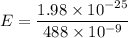
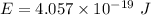
Converting Joules (J) to eV ; we get,
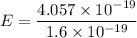
E = 2.53 eV
The energy levels of the first exited state = -13.223 eV