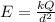Answer:
The relationship is
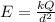
Step-by-step explanation:
The electric field strength is denoted by the symbol E,
the test charge is denoted be q and the source charge be Q
distance is denoted by d
Then the equation can be rewritten in symbolic form as
Electric field strength is = Force/charge

we know that the formula for force is given as
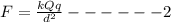
where
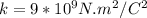
and d is the separation distance between charges
We can insert the expression for Force in equation one
we have

We can strike out both qs in the numerator and denominator we have