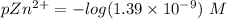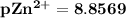Answer:
Step-by-step explanation:
Using the approach of Henderson-HasselBalch equation, we have :
![pH = pKa[NH^+_4] + log ([NH_3])/([NH_4^+])](https://img.qammunity.org/2021/formulas/chemistry/college/tk4x7q7ka5lfvpclsgvrd18nkloe8nnqvt.png)
where;
the pKa of
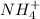 = 9.26
= 9.26
concentration of
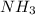 = 0.100 M
= 0.100 M
concentration of
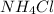 = 0.176 M
= 0.176 M
∴
the pH of the buffered solution is :
![pH = 9.26 + log ([0.100])/([0.176])](https://img.qammunity.org/2021/formulas/chemistry/college/mc466ce18ms80xxyfpn2578jn02d7srfet.png)
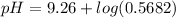
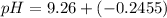
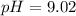
The Chemical equation for the reaction of
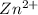 and EDTA is :
and EDTA is :

Here;
 denotes the fully deprotonated form of the EDTA
denotes the fully deprotonated form of the EDTA
The formation constant
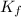 of the equation for the reaction can be represented as:
of the equation for the reaction can be represented as:
![K_f = ([ZnY^(2-)])/([Zn^(2+) ][Y^(4-)])](https://img.qammunity.org/2021/formulas/chemistry/college/g7jkm0hvhjwf00l4nv209f9fca8xj607k3.png) ----- (1)
----- (1)
The logarithm of the formation constant of Zn - EDTA complex = 16.5
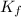 =
=
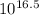
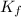 =
=
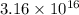
Since the formation constant in the above equation signifies that the EDTA is present in
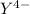 ,
,
Then:

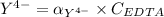
From (1)
![K_f = ([ZnY^(2-)])/([Zn^(2+) ][Y^(4-)])](https://img.qammunity.org/2021/formulas/chemistry/college/g7jkm0hvhjwf00l4nv209f9fca8xj607k3.png)
![K_f = \frac{[ZnY^(2-)]}{[Zn^(2+) ] \ \ \alpha_ {Y^(4-)} * {C_(EDTA)}}](https://img.qammunity.org/2021/formulas/chemistry/college/tc737goa0i16arcx6z6nprqh43f45fwn6o.png)
∴
![K_f' = K_f * \alpha _Y{^4-} = ([ZnY^(2-)])/([Zn^(2+) ] \ C_(EDTA) )](https://img.qammunity.org/2021/formulas/chemistry/college/k6mp4d3xcguflrhokycuk77l8lqzx1k0m7.png)
where;
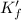 = conditional formation constant
= conditional formation constant
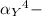 = the fraction of EDTA that exit in the form of the presences of the 4 charges .
= the fraction of EDTA that exit in the form of the presences of the 4 charges .
So at equivalence point :
all the
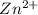 initially in titrand is now present in
initially in titrand is now present in

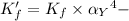
Obtaining the data for the value of
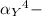 at the reference table:
at the reference table:
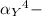 =
=

∴
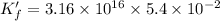
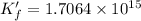
To calculate the moles of EDTA ,
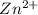 ,
,
 ; we have:
; we have:
moles of EDTA = 0.0100 M × 0.025 L
moles of EDTA =

moles of
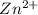 = 0.00500 M × 0.050 L
= 0.00500 M × 0.050 L
moles of
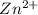 =
=

moles of
 =
=
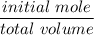
moles of
 =
=
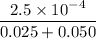
moles of
 =
=
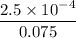
moles of
 = 0.0033333 M
= 0.0033333 M
Recall that:
![K_f' = K_f * \alpha _Y{^4-} = ([ZnY^(2-)])/([Zn^(2+) ] \ C_(EDTA) )](https://img.qammunity.org/2021/formulas/chemistry/college/k6mp4d3xcguflrhokycuk77l8lqzx1k0m7.png)
![K_f' = ([ZnY^(2-)])/([Zn^(2+) ] \ C_(EDTA) )](https://img.qammunity.org/2021/formulas/chemistry/college/hmp6ol2800mauuowkv36qtvojspj5sexmk.png)
Assume Q² is the amount of complex dissociated in

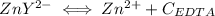
i.e
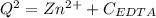
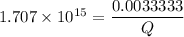
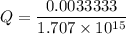

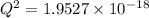
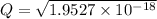
Q =
 M
M
![[Zn^(2+)]= 1.39 * 10^(-9) \ M](https://img.qammunity.org/2021/formulas/chemistry/college/rmktacuairzv7r6oibg1yqh6zy2we1fu8h.png)
∴
![pZn ^(2+) =- log [Zn^(2+)]](https://img.qammunity.org/2021/formulas/chemistry/college/9h5ut4krmsi2455ea5arlynbqbpf3yd2gn.png)