Answer:
By using The Pythagorean Theorem:
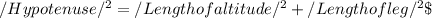
/Hypotenuse/ =
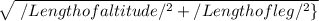
Explanation:
The Pythagorean theorem states that: Given a Right-angled triangle, the square of the hypotenuse equals the sum of squares of the other two sides ( Here, being the length of the altitude and length of leg). That is,
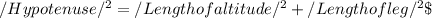 and hence,
and hence,
/Hypotenuse/ =
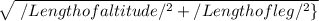
For example, If the length of the altitude is 4m and the length of leg is 3m. Using The Pythagorean theorem, the length of the hypotenuse will be
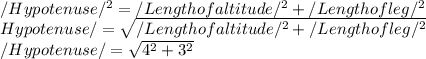
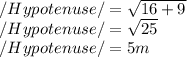
The length of the hypotenuse for the given example will be 5m.
This is how to find the length of an hypotenuse.