Question

A man weighing 700 NN and a woman weighing 440 NN have the same momentum. What is the ratio of the man's kinetic energy KmKmK_m to that of the woman K

Answer 1

The ratio of the man's kinetic energy to that of the woman's kinetic energy is 0.629.

Step-by-step explanation:

Given;

weight of the man, W = 700 N

Weight of the woman, W = 440 N

momentum is given by;

`P = mv\\\\v = (P)/(m)`

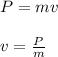
Kinetic energy of the man;

`K_m = (1)/(2)m_m((P_m)/(m_m))^2 \\\\K_m = (P_m^2)/(2m_m)`

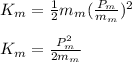
Momentum of the man is calculated as;

`P_m^2 = 2m_mK_m`

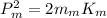
The kinetic energy of the woman is given by;

`K_w = (P_w^2)/(2m_w)`

The momentum of the woman is given;

`P_w^2 = 2m_wK_w`

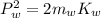
Since, momentum of the man = momentum of the woman

`P_m^2 = P_w^2`

`2m_mK_m = 2m_wK_w\\\\(K_m)/(K_w) = (2m_w)/(2m_m)\\\\(K_m)/(K_w) = (m_w)/(m_m)`

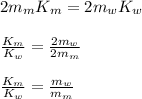
mass of the mas = 700 / 9.8 = 71.429

mass of the woman is = 440 / 9.8 = 44.898

`(K_m)/(K_w) = (44.898)/(71.429)\\\\(K_m)/(K_w) =0.629`

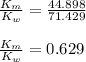
Therefore, the ratio of the man's kinetic energy to that of the woman's kinetic energy is 0.629.