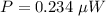Question

A mobile base station (BS) in an urban environment has a power measurement of 15 µW at 175 m. If the propagation follows an inverse cube-power law (Section 3.2.2), what is a reasonable power value, in µW, to assume at a distance 0.7 km from the BS?

Answer 1

The reasonable power will be "0.234 μW".

Step-by-step explanation:

The given values are:

P = 15 μW

d = 175 m

As we know,

Propagation follows inverse cube power law, then

∴
`Power \ \alpha \ (1)/(d^3)`

⇒
`Power=(K)/(d^3)`

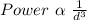
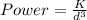
On substituting the estimated values, we get

⇒
`15* 10^(-6)=(K)/((173)^3)`

⇒
`K=15* (175)^3* 10^(-6)`

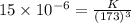
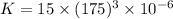
Now,

"P" at 0.7 km or 700 m from BS will be:

⇒
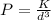
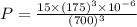
`P=(K)/(d^3)`

⇒
`P=(15* (175)^3* 10^(-6))/((700)^3)`

⇒
`P=0.234 \ \mu W`