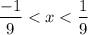Answer:
The series converges to
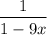 for
for
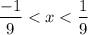
Explanation:
Given the series is
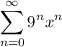
We have to find the values of x for which the series converges.
We know,
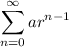 converges to (a) / (1-r) if r < 1
converges to (a) / (1-r) if r < 1
Otherwise the series will diverge.
Here,
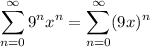 is a geometric series with |r| = | 9x |
is a geometric series with |r| = | 9x |
And it converges for |9x| < 1
Hence, the given series gets converge for
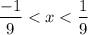
And geometric series converges to
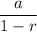
Here, a = 1 and r = 9x
Therefore,
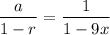
Hence, the given series converges to
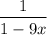 for
for