Question

Find all values of x for which the series converges. (Enter your answer using interval notation.) [infinity] 9 x − 7 9 n n = 0 For these values of x, write the sum of the series as a function of x.

Answer 1

The series converges to
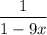`$ (1)/(1-9x) $` for
`$ (-1)/(9) < x < (1)/(9) $`

Explanation:

Given the series is
`$ \sum_(n=0)^(\infty) 9^n x^n $`

We have to find the values of x for which the series converges.

We know,

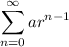`$ \sum_(n=0)^(\infty) ar^(n-1) $` converges to (a) / (1-r) if r < 1

Otherwise the series will diverge.

Here,
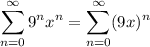`$ \sum_(n=0)^(\infty) 9^n x^n = \sum_(n=0)^(\infty) (9x)^(n) $` is a geometric series with |r| = | 9x |

And it converges for |9x| < 1

Hence, the given series gets converge for
`$ (-1)/(9) < x < (1)/(9) $`

And geometric series converges to
`$ (a)/(1-r) $`

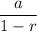
Here, a = 1 and r = 9x

Therefore,
`$ (a)/(1-r) = (1)/(1-9x) $`

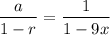
Hence, the given series converges to
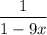`$ (1)/(1-9x) $` for
`$ (-1)/(9) < x < (1)/(9) $`