Question

Solve each equation using the Zero Product Property and the Distributive Property (as necessary)

11. f(x)=3x(2x-6)

12. f(x)=3x(x+7)-2(x+7)

Answer 1

`\large \boxed{{\bold{11.} \ x=0, \ x=3}} \\ \\ \large \boxed{{\bold{12.} \ x=-7, \ x=2/3}}`

Explanation:

We will set the outputs of the functions to 0 and solve for x.

0 = 3x(2x - 6)

Set factors equal to 0.

First possibility:

3x = 0

x = 0

Second possibility:

2x - 6 = 0

2x = 6

x = 3

0=3x(x+7)-2(x+7)

Take (x+7) as a common factor.

0 = (3x-2)(x+7)

Set factors equal to 0.

First possibility:

x + 7 = 0

x = -7

Second possibility:

3x - 2 = 0

3x = 2

x = 2/3

Answer 2

11) x=1 or x=3.

12) x=2/3 or x=-7.

Explanation:

So we have two equations:

`f(x)=3x(2x-6)\\f(x)=3x(x+7)-2(x+7)`

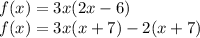
And we want to solve them. To do so, make each of them equal 0 and then solve for x:

11)

`f(x)=3x(2x-6)\\0=3x(2x-6)`

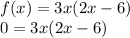
Using the Zero Product Property, either one or both of the factor must be zero for this to be true. Therefore, make each factor equal to zero and solve:

`3x=0 \text{ or } 2x-6=0`

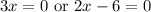
Divide the left by 3. On the right, add 6 and then divide by 2:

`x=0\text{ or } 2x=6\\x=0 \text{ or } x=3`

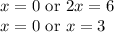
Therefore, the solutions to the first equation is:

x=1 or x=3.

12)

`f(x)=3x(x+7)-2(x+7)`

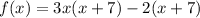
First, use the distributive property to group the terms together. The equation is equivalent to:

`f(x)=(3x-2)(x+7)`

Now, set the function to zero and solve:

`0=(3x-2)(x+7)`

`(3x-2)=0 \text{ or } x+7=0\\3x=2 \text{ or } x=-7\\x=2/3 \text{ or } x=-7.`

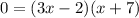
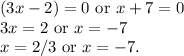
Therefore, the answer is:

x=2/3 or x=-7.