Answer:
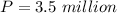
Explanation:
Given
Represent 1950 Population with P and 2003 Population with Q
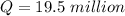
Required
Determine the value of P
From the question; we have that
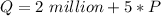
Substitute 19.5 million for Q
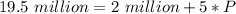
Subtract 2 million from both sides

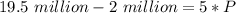
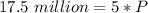
Divide both sides by 5

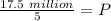
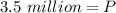
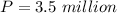
Hence, the 1950 population is 3.5 million