Question

Sandra calculated the height of a cylinder that has a volume of 576 pi cubic centimeters and a radius of 8 centimeters. Her work is shown below. V = B h Step 1: 576 pi = pi 8 squared h Step 2: 576 pi = 64 pi h Step 3: StartFraction 576 pi Over 64 pi EndFraction = StartFraction 64 pi Over 64 pi EndFraction h Step 4: h = 9 pi cm What error did Sandra make when calculating the height of the cylinder? In step 1, she substituted into the volume formula incorrectly. In step 2, she calculated 8 squared incorrectly. It should be 16 rather than 64. In step 4, the pi should have canceled, making the correct answer 9 cm. Sandra calculated the height of the cylinder correctly.

Answer 1

(C) In step 4, the pi should have canceled, making the correct answer 9 cm.

Answer 2

The error was made in step 4,
`\pi` should have also been cancelled making the correct answer as 9 cm.

Explanation:

Given that:

Volume of cylinder,
`V = 576 \pi\ cm^3`

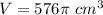
Radius of cylinder, r = 8 cm

To find:

The error in calculating the height of cylinder by Sandra ?

Solution:

We know that volume of a cylinder is given as:

`V = B h`

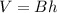
Where B is the area of circular base and

h is the height of cylinder.

Area of a circle is given as,
`B = \pi r^2`

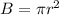
Let us put it in the formula of volume:

`V = \pi r^2 h`

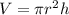
Step 1:

Putting the values of V and r:

`576\pi = \pi 8^2 h`

So, it is correct.

Step 2:

Solving square of 8:

`576\pi = \pi * 64* h`

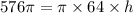
So, step 2 is also correct.

Step 3:

`h=(576\pi)/(64 \pi) = (64 \pi * 9)/(64\pi)`

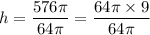
Step 4:

Cancelling 64
`* \pi`,

h = 9 cm

So, the error was made in step 4,
`\pi` should have also been cancelled making the correct answer as 9 cm.