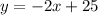Question

- Find the slope intercept form of the equation. 4x + 2y = 50
​

Answer 1

`y=-2x+25`

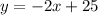
Explanation:

To find the slope-intercept form of the equation, we just need to isolate the y-variable.

So we have the equation:

`4x+2y=50`

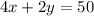
First, subtract 4x from both sides. The 4xs on the left cancel:

`(4x+2y)-4x=50-4x\\2y=-4x+50`

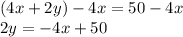
Now, divide both sides by 2. The 2s on the left cancel:

`(2y)/(2)=(-4x+50)/(2) \\y=(-4x+50)/(2)`

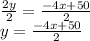
Simplify the right side. Expand the fraction:

`y=(-4x)/(2)+(50)/(2) \\`

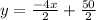
Cancel out the terms:

`y=-2x+25`

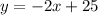
Therefore, the slope-intercept form is:

`y=-2x+25`

Answer 2

`\boxed{y=-2x+25}`

Explanation:

First, subtract 4x from both sides of the equation to put into slope-intercept form (y = mx + b). Then, divide by 2 to isolate the y.

4x + 2y = 50

2y = -4x + 50

y = -2x + 25