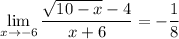Answer:
Explanation:
We want to evaluate the limit:
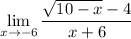
When attempting to evaluate a limit, we should always try direct substitution. This yields:
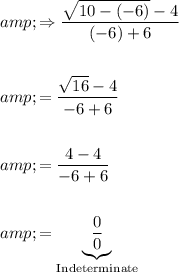
Since the result is an indeterminate form, we can try simplifying the limit.
Let's cancel the square root in the numerator. We can use the difference of two squares. Recall that:
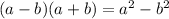
The expression in the numerator is:
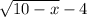
Therefore, to cancel it out, we will multiply it by:
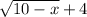
Multiply. This yields:
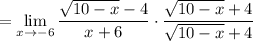
Simplify:
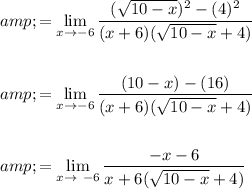
Factor:
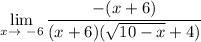
Cancel:
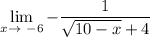
Now, we can attempt direct substitution again. Thus:
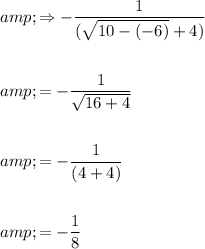
Therefore: