Question

I need help with rational and irrational numbers here is the question.

Select all true statements about the square root of 2.

-It is a real number.
-It is an irrational number.
-It is a rational number.
-It is an integer.
-It is not a real number.

Answer 1

`\Large \boxed{\mathrm{It \ is \ a \ real \ number.}} \\ \\ \Large \boxed{\mathrm{It \ is \ an \ irrational \ number.}}`

Explanation:

`√(2)`

Real numbers includes all the rational and irrational numbers.

Not real numbers include all the imaginary numbers.

Integers includes all whole numbers that are negative, positive, or zero.

Rational numbers can be expressed as the quotient of two integers.

Irrational numbers cannot be expressed as the quotient of two integers.

`√(2)= 1.41421356237......`

The result of square root of 2 keeps going on.

It cannot be expressed as the quotient of two integers.

Therefore, the square root of 2 is an irrational number.

It is a real number since it is an irrational number.

Answer 2

The correct answer choices are:

1) It is a real number

2) It is an irrational number

Explanation:

So we have the number:

`\sqrt2`

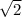
First, let's define each of the terms:

Real numbers are all of the irrational and rational numbers. If a number is irrational or rational, then they are a real number. Any number that does not include the imaginary number i is real (you'll learn this eventually. It's actually really interesting!).

Irrational numbers are the numbers that do not terminate nor repeat. Examples include π or √3. Note that numbers like 1/3 which is .3333 is not irrational because they are repeating. π, on the other hand, does not repeat and never ends.

Rational numbers are the numbers that terminate or repeat. They also include the integers, whole numbers, and natural numbers.

So, the √2. First, it's real because it doesn't deal with imaginaries.

Next, use a calculator and calculate √2. We can see that it is about 1.41423562... This number does not repeat. And it does not terminate (end). In other words, √2 is a irrational numbers.

Since it is irrational, it cannot be rational. Since it's not rational, it cannot be an integer, whole number, or a natural number.

Therefore, the correct answer choices are:

1) It is a real number

2) It is an irrational number