Question

A 15g block is sliding along horizontal plane and is given an initial velocity. The coefficient of kinetic friction between the plane and the block is 0.3. How far does the block travel before coming to a complete stop?

Answer 1

3.67 meters

Step-by-step explanation:

The question is incomplete without a value for the initial velocity, which i assume you meant to say it is 4.65 m/s

we will begin by applying the newtons second law of motion stated below

`v^2 - u^2 = 2as`

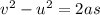
Given data

v = 0

u= 4.65 m/s

m= 15 g= 0.015 kg

μ= 0.3

we know that F= ma

a = F/m

also F= -μR

and R= mg

i.e F= μmg

hence

a= -μmg/m = -μg [minus sign because the acceleration is opposite the direction of motion]

Making s subject of formula we have

0 - u^2 = 2(-μg)s

s = U^2 / (2μg)

Substituting in the second equation of motion we have

`=((4.65)^2)/( 2(0.3)(9.81) ) \\\\\ = \frac {21.62}{ 5.88 } \\\\ =3.67 m`

The block will go 3.67 meters before stopping