Question

Find dy/dx and d2y/dx2, and find the slope and concavity (if possible) at the given value of the parameter. (If an answer does not exist, enter DNE.) Parametric Equations Point x = 6t, y = 4t − 3 t = 4

Answer 1

The slope of the function is ²/₃ and since the second derivative is zero, the concavity doesn't exist.

Explanation:

Given;

x = 6t

y = 4t - 3

point t = 4

`(dy)/(dx) = ((dy)/(dt) )/((dx)/(dt) )=((dy)/(dt) )/((dx)/(dt)) \\\\(dy)/(dt) = 4; (dx)/(dt) = 6\\\\(dy)/(dx) =(4)/(6) = (2)/(3)`

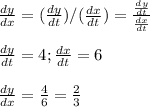
The slope of the function is ²/₃

take the second derivative of the function;

the second derivative will be zero since the first derivative is a constant value.

`(d^2y)/(dx^2) = 0`

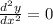
Since the second derivative is zero, the concavity doesn't exist.