Question

Suppose an operator handles 10 calls. What is the probability that none of the 10 calls result in a reservation?

Answer 1

To find the probability that none of the 10 calls result in a reservation, you can multiply the probability of a call not resulting in a reservation by itself 10 times.

Step-by-step explanation:

To find the probability that none of the 10 calls result in a reservation, we need to determine the probability that each individual call does not result in a reservation and multiply those probabilities together.

Let's assume that the probability of a call resulting in a reservation is p. Therefore, the probability of a call not resulting in a reservation is 1-p.

Since we want to find the probability of none of the 10 calls resulting in a reservation, we can multiply (1-p) by itself 10 times.

Therefore, the probability that none of the 10 calls result in a reservation is
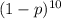`(1-p)^{10`.

Answer 2

Question:

Approximately 30% of the calls to an airline reservation phone line result in a reservation being made. Suppose that an operator handles 10 calls. What is the probability that none of the 10 calls result in a reservation?

Answer:

`Probability = 0.028`

Step-by-step explanation:

Given

Represent probability of reservation with p and Number of calls with n

`n= 10`

`p = 30\%`

First, we need to convert p to decimal

`p = (30)/(100)`

`p = 0.30`

In probability; opposite probability add up to 1;

In other words,

`p + q = 1`

Where q represents probability of no reservation

Substitute 0.30 for p

`0.30 + q = 1`

`q = 1 - 0.30`

`q = 0.70`

The probability that out of the 10 calls, no reservation is made is calculated as;

`Probability = q^n`

`Probability = 0.70^(10)`

`Probability = 0.0282475249`

`Probability = 0.028` (Approximated)