Answer:
Slope-Intercept form: y=3x+7
Standard form: 3x-y=-7
Point-slope form: y-1=3(x+2)
Explanation:
Slope-Intercept form:
First, find the slope, using the formula:
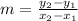
Our x₁ and y₁ will be the point (-2,1) and our x₂ and y₂ wwill be the point (1,10).
So let's write those in our equation to find slope:
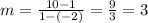
Therefore, our slope is 3.
Now let's write our linear equation with what we have already in slope-intercept form:
y=3x+b
Well, we still need to find the y-intercept, or "b".
Plug in one of your points for the x and y values of the equation. We'll use the point (-2,1)
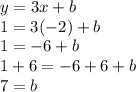
This means our y-intercept is 7. Now we can write our equation in slope-intercept form completely:
y=3x+7
Standard form:
Now, let's find this equation is standard form.
Take your equation in slope-intercept form and write it out again:
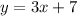
Now, standard form of a linear equation is ax+by=c, so subtract 3x from both sides:
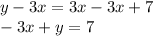
The "a" coefficient in standard form cannot be negative, so divide the entire equation by -1:
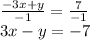
Therefore, your equation in standad form is:
3x-y=-7
Point-Slope form:
The formula for point-slope form is y-y₁=m(x-x₁). We already know that our x₁ and y₁ is the point (-2,1) and we know that our slope, m, is 3, so we just have to plug then in where the fit in the equation.
x₁ is -2 and y₁ is 1 and m is 3, so:
y-1=3(x-(-2)) or y-1=3(x+2)
That means our equation in point-slope form is:
y-1=3(x+2)