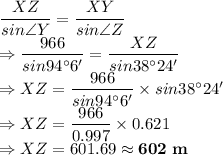Question

to find the distance between a point x and an inaccessible point​ z, a line segment xy is constructed. measurements show that xy=966 ​m, angle xyz​=38°24', and angle yzx=94°6'. find the distance between x and z to the nearest meter.

Answer 1

`\approx \bold{602\ m}`

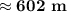
Explanation:

Given the following dimensions:

XY=966 ​m

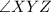`\angle XYZ`​ = 38°24', and

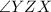`\angle YZX` = 94°6'

To find:

Distance between points X and Z.

Solution:

Let us plot the given values.

We can clearly see that it forms a triangle when we join the points X to Y, Y to Z and Z to X.

The
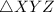`\triangle XYZ` has following dimensions:

XY=966 ​m

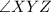`\angle XYZ`​ = 38°24', and

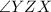`\angle YZX` = 94°6'

in which we have to find the side XZ.

Kindly refer to the image attached.

Let us use the Sine rule here:

As per Sine Rule:

`(a)/(sinA) = (b)/(sinB) = (c)/(sinC)`

Where

a is the side opposite to
`\angle A`

b is the side opposite to
`\angle B`

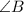
c is the side opposite to
`\angle C`

`(XZ)/(sin\angle Y) = (XY)/(sin\angle Z)\\\Rightarrow (966)/(sin94^\circ6') = (XZ)/(sin38^\circ24')\\\Rightarrow XZ=(966)/(sin94^\circ6') * sin38^\circ24'\\\Rightarrow XZ=(966)/(0.997) * 0.621\\\Rightarrow XZ=601.69 \m \approx \bold{602\ m}`