Answer/Step-by-step Explanation:
a. Order the marks scored by James from the least to the largest:
11, 12, 13, 13, 16, 17, 17, 18, 19, 19, 20
To find the interquartile range for James Marks, first find the median, Q1, and then Q3.
The median is the middle value, which is the 6th value in the data set.
11, 12, 13, 13, 16, [17], 17, 18, 19, 19, 20
The median = 17
The Q1 is the middle value from the median to your left, while Q3 is the middle value from the median to the right.
11, 12, (13), 13, 16, [17], 17, 18, (19), 19, 20
Q1 = 13
Q3 = 19
Interquartile range (IQR) =
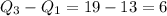
b. Sunil has a median score of 17, which is the same has that of James, however, the interquartile range value for that of Sunil is higher (8) than that of James (6).
The higher the interquartile range, the much variation there is in a set of data. Which can imply inconsistency.
Therefore, James has more consistent marks because his marks has lesser variation.
c. The new marks of the tests which are 16, 20, 18, and 10, would not change the initial median score. This is because, 10 and 16 would fall under the initial median value of 17, while 18 and 20 would fall above the median value of 17. The data set would still be divided into 2, with 17 still being the median.
Therefore, the new median is 17.