Question

Solve the system by using a matrix equation.
--4x - 5y = -5
-6x - 8y = -2

Answer 1

Solution : (15, - 11)

Explanation:

We want to solve this problem using a matrix, so it would be wise to apply Gaussian elimination. Doing so we can start by writing out the matrix of the coefficients, and the solutions ( - 5 and - 2 ) --- ( 1 )

`\begin{bmatrix}-4&-5&|&-5\\ -6&-8&|&-2\end{bmatrix}`

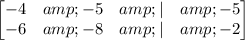
Now let's begin by canceling the leading coefficient in each row, reaching row echelon form, as we desire --- ( 2 )

Row Echelon Form :

`\begin{pmatrix}1\:&\:\cdots \:&\:b\:\\ 0\:&\ddots \:&\:\vdots \\ 0\:&\:0\:&\:1\end{pmatrix}`

Step # 1 : Swap the first and second matrix rows,

`\begin{pmatrix}-6&-8&-2\\ -4&-5&-5\end{pmatrix}`

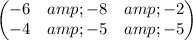
Step # 2 : Cancel leading coefficient in row 2 through
`R_2\:\leftarrow \:R_2-(2)/(3)\cdot \:R_1`,

`\begin{pmatrix}-6&-8&-2\\ 0&(1)/(3)&-(11)/(3)\end{pmatrix}`

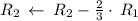Now we can continue canceling the leading coefficient in each row, and finally reach the following matrix.

`\begin{bmatrix}1&0&|&15\\ 0&1&|&-11\end{bmatrix}`

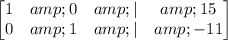
As you can see our solution is x = 15, y = - 11 or (15, - 11).