Question

Which statement best explains why the sine of an acute angle is equal to the cosine of the angles complement

Answer 1

Option (B)

Explanation:

From the figure attached,

ΔABC is a right triangle.

Cosine and Sine ratios from the given triangle will be,

SinA =
`\frac{\text{Opposite side}}{Hypotenuse}`

=
`(a)/(c)`

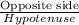
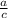
CosB =
`\frac{\text{Adjacent side}}{\text{Hypotenuse}}`

=
`(a)/(c)`

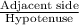
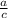
Therefore, both the ratios (Sine and Cosine) will be equal as
`(a)/(c)`

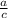
Option (B) will be the correct option.