Question

What is the solution of x⁴– 3x³ + x²+ 3x – 2 < 0

Answer 1

Hello, let's note

`f(x)=x^4-3x^3+x^2+3x-2\\\\f(1)=1-3+1+3-2=0`

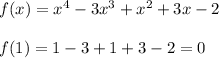
So we can put (x-1) in factor. We are looking for a and b such that

`f(x)=(x-1)(x^3+ax^2+bx+2)=x^4+(a-1)x^3+(b-a)x^2+(2-b)x-2`

We identify the like terms, it comes

a-1=-3 <=> a = -2

b-a=1 <=> b = 1 + a = -1

2-b=3

So it comes.

`f(x)=(x-1)(x^3-2x^2-x+2)`

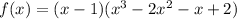
And we can go further using the same method to find that

`x^3-2x^2-x+2=(x-1)(x^2-x-2)`

The sum of the zeroes is 1=2-1 and the product is -2=(-1)*2, so, we can factorise.

`\boxed{f(x)=(x-1)^2(x+1)(x-2)}`

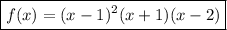
The sign of f(x) is the same as the sign of (x+1)(x-2) as a square is always positive.

To find the sign of a product, we can apply the following.

"- multiplied by - gives +"

"+ multiplied by + gives +"

"- multiplied by + gives -"

"+ multiplied by - gives -"

This is this what we are doing below.

So, to answer the question

`\Large \boxed{\sf \bf \ f(x) < 0 <=> -1 < x < 2 \ }`

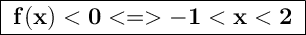
Thank you.