Question

A ball is thrown vertically upward from the top of a tower 40m high with velocity 10m/sec find time when it strikes ground

​

Answer 1

Given:-

• Height,h = -40 m

• Initial velocity,u = 10 m/s

• Final velocity,v = 0

• Acceleration due to gravity,g = -10 m/s² [ Ball goes up ]

To find out:-

Find time when it strikes ground.

Formula used:-

s = ut + 1/2 at²

Solution:-

We will first calculate the time taken by the ball to reach the highest point by using the formula:

S = ut + 1/2 at²

★ Substituting the values in the above formula,we get:

⇒ -40 = 10 × t + 1/2 × -10 × t²

⇒ -40 = 10t + ( - 5 ) × t²

⇒ -40 = 10t - 5 t²

⇒ 5t² - 10t - 40

⇒ 5t² - 20t + 10t - 40

⇒ 5t ( t - 4 ) + 10 ( t - 4 )

⇒ t - 4 = 0 and 5t + 10 = 0

⇒ t = 4 and t = -2

Thus,time taken is 4 seconds. [ Ignore negative number. ]

Answer 2

`\Huge \boxed{\mathrm{4 \ s}}`

Step-by-step explanation:

Displacement ⇒ -40 m (the ball strikes the ground)

Initial velocity ⇒ 10 m/s

Acceleration of gravity ⇒ -10 m/s² (upward acceleration)

We can use a formula to find the time taken.

`s = ut + 1/2 at^2`

`s = \sf displacement \ (m)`

`u = \sf initial \ velocity \ (m/s)`

`a = \sf acceleration \ of \ gravity \ (m/s^2)`

`t = \sf time \ taken \ (s)`

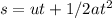
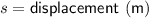
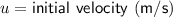
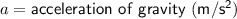
Plugging in the values.

`-40 = (10)t + 1/2 (-10)t^2`

Solve for
`t`.

`-40 = 10t-5t^2`

`5t^2-10t-40=0`

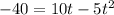
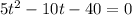
Factor the quadratic expression.

`5(t+2)(t-4)=0`

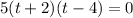
Set the factors equal to 0.

`t+2=0\\t=-2`

`t-4=0\\t=4`

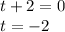
t = -2 and t = 4 (time value will not be negative in this case)

The time the ball takes to strike the ground is 4 seconds.