Question

Evaluate the expression

Answer 1

`12-[20-2(6^2/3*2^2)]=88`

Explanation:

So we have the expression:

`12-[20-2(6^2/3*2^2)]`

Recall the order of operations or PEMDAS:

P: Operations within parentheses must be done first. On a side note, do parentheses before brackets.

E: Within the parentheses, if exponents are present, do them before all other operations.

M/D: Multiplication and division next, whichever comes first.

A/S: Addition and subtraction next, whichever comes first.

(Note: This is how the order of operations is traditionally taught and how it was to me. If this is different for you, I do apologize. However, the answer should be the same.)

Thus, we should do the operations inside the parentheses first. Therefore:

`12-[20-2(6^2/3*2^2)]`

The parentheses is:

`(6^2/3*2^2)`

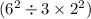
Square the 6 and the 4:

`(36/3*4)`

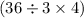
Do the operations from left to right. 36 divided by 3 is 12. 12 times 4 is 48:

`(36/3*4)\\=(12*4)\\=48`

Therefore, the original equation is now:

`12-[20-2(6^2/3*2^2)]\\=12- [20-2(48)]`

Multiply with the brackets:

`=12-[20-96]`

Subtract with the brackets:

`=12-[-76]`

Two negatives make a positive. Add:

`=12+76=88`

Therefore:

`12-[20-2(6^2/3*2^2)]=88`