Question

Solve 3x+2y−z=2 2y+z=7 −2x−4z=−2 Enter your answer, in the form (x,y,z), in the boxes in simplest terms. x= y= z=

Answer 1

(x, y, z) = (-1, 3, 1)

Explanation:

Any of a number of web sites will solve systems of equations for you. Your graphing calculator will, too.

The solution is the right-most column in reduced row echelon form. Top to bottom, the variables are in order x, y, z.

(x, y, z) = (-1, 3, 1)

_____

If you like, you can use substitution to do this by hand.

z = 3x +2y -2 . . . . from the first equation

2y +(3x +2y -2) = 7 . . . . substituting into the second equation

3x +4y = 9 . . . . . in standard form

-2x -4(3x +2y -2) = -2 . . . . substituting for z into the third equation

14x +8y = 10 . . . . . in standard form

Subtract half the second equation from the first:

(3x +4y) -(7x +4y) = (9) -(5)

-4x = 4 . . . simplify

x = -1 . . . . . divide by 4

y = (9 -3x)/4 = (9 -3(-1))/4 = 12/4 = 3

z = 3(-1) +2(3) -2 = 1

The solution is (x, y, z) = (-1, 3, 1).

Answer 2

(-1, 3, 1)

x=-1, y=3, z=1.

Explanation:

So we have the three equations:

`3x+2y-z=2\\2y+z=7\\-2x-4z=-2`

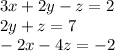
And we want to find the value of each variable.

To do so, look at the equations and try to think about what we can do to isolate one of the variables by itself.

We can see that both the second and equation has a variable and then the variable z.

In other words, we can solve for y in the second equation and x in the third equation and then substitute them in the first equation to isolate the variable z and then solve for z. With that, we can then easily arrive at our solution.

Therefore, solve for y in the second equation:

`2y+z=7`

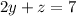
Subtract z from both sides. The zs on the left side cancels:

`(2y+z)-z=(7)-z\\2y=7-z`

Now, divide both sides by 2. The 2s on the left cancel and we've isolated the y variable:

`((2y))/(2) = ((7-z))/(2)\\y=((7-z))/(2)`

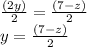
Now, do the same for the third equation. Isolate the x variable:

`-2x-4z=-2`

First, divide everything by -2 to make things simpler:

`((-2x-4z))/(-2)=((-2))/(-2)\\ x+2z=1`

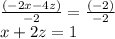
Now, subtract 2z from both sides to isolate the x variable:

`(x+2z)-2z=1-2z\\x=1-2z`

We have isolated the x and y variables. They are:

`y=((7-z))/(2)\\x=1-2z`

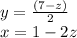
Now, we can substitute them back into the first equation. Therefore:

`3x+2y-z=2\\3(1-2z)+2((7-z)/(2))-z=2`

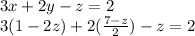
Distribute the first and second terms. The second term cancels out:

`3(1)-3(2z)+(7-z)-z=2\\3-6z+7-z-z=2`

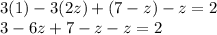
Combine like terms:

`-6z-z-z+3+7=2\\-8z+10=2\\`

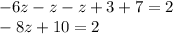
Subtract 10 from both sides:

`(-8z+10)-10=2-10\\-8z=-8`

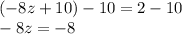
Divide both sides by -8:

`z=1`

Now that we've determined that z=1, plug it back into the isolated second and third equations:

Second equation:

`y=((7-z))/(2)\\y=(7-1)/2\\y=(6)/2=3`

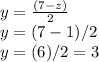
Third equation:

`x=1-2z\\x=1-2(1)\\x=1-2=-1`

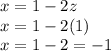
Therefore, our answer is (-1, 3, 1)