Question

Let a metallic rod 20 cm in length be heated to a uniform temperature of 100°C Suppose that at t=0 the ends of the bar are plunged into an ice bath at 0°C and thereafter maintained at this temperature, but that no heat is allowed to escape through the lateral surface. Find the time that will elapse before the center of the bar cools to a temperature of 5°C if the bar is made of (a) silver (b) aluminum (c) cast iron. The α2 values for silver, aluminum and cast iron are 1.71, 0.86 and 0.12 respectively.

(Round your answer to two decimal places. Use two-term approximation of the series.)
For silver, it takes _____ seconds to cool the bar to a temperature of 5°C
For aluminum, it takes _____ seconds to cool the bar to a temperature of 5°C
For cast iron, it takes _____ seconds to cool the bar to a temperature of 5°C

Answer 1

a) t = 59 s , b) t = 107 s , c) t = 466 s

Step-by-step explanation:

This is an exercise in thermal conductivity. The power dissipated or transferred is

P = Q / Δt = k A dT/dx

where Q is the thermal energy of the bar, k the constant of thermal conductivity.

If we assume that we are in a stable regime

dT / dx = (T₀ -
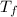`T_(f)`) / L

the energy in the bar is

Q = m
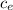`c_(e)` T₀

we substitute

m c_{e} T₀ / t = k A (T₀ -T_{f}) / L

t = c_{e} / k m L / A T₀ / (T₀ -T_{f})

let's use the concept of density

ρ = m / V

V = A L

m = ρ AL

t = c_{e} / k (ρ A L) L / A T₀ / (T₀ -T_{f})

t =
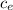`c_(e)` /k ρ L² T₀/(T₀ -T_{f})

In this exercise, the initial temperature is T₀ = 100ºC, the final temperature is T_{f }= 5ºC and the length

L = L₀ / 2 = 20/2 = 10cm = 0.1m

a) case of silver

c_{e} = 234 J / kg ºC

k = 437 W / m ºC

ρ = 10,490 10³ kg / m³

let's calculate

t = 234/437 10.49 10³ 0.1² 100 / (100 -5)

t = 59 s

b) case materials aluminum

c_{e} = 900 J / kg ºC

k = 238 W / m ºC

ρ = 2.70 10³ kg / m³

t = 900/238 2.70 10³ 0.1² 100 / (100-5)

t = 107 s

c) iron material

c_{e} = 448 J / kg ºC

k = 79.5 W / m ºC

ρ = 7.86 10³ kg / m³

t = 448 / 79.5 7.86 10³ 0.1² 100 / (100-5)

t = 466 s